SIM-NANOPORE
Molecular
simulations for penetrable fluids confined in nanopore systems
Program
Capacities/Module III – Bilateral cooperation 462
/ 18.02.2011
Type
of project: Bilateral
Partner
countries: Romania – South Korea
Period
of collaboration: March 2011 – December 2011
PARTNERS
-
|
Coordinators:
|
|
Dr.
Viorel Chihaia
Institute
of Physical Chemistry “Ilie Murgulescu”, Romanian
Academy
Splaiul
Independentei 202, 060021, Bucharest
Phone
(+40) 021-316-7912
e-mail:
vchihaia@icf.ro
|
Prof. Soong-Hyuck
Suh
Keimyung
University, Department of Chemical Engineering
#1,000
Shindang-dong, Dalseo-ku, Daegu, 704-701, Republic of Korea
e-mail:
shsuh@kmu.ac.kr
|
|
|
|
Teams:
|
|
Dr.
Popa Vlad
|
Prof.
Jae-Young Bae
|
|
Dr.
Munteanu Gabriel
|
Prof.
Kwan-Kyu Park
|
|
Dr.
Stanica Nicolae
|
Prof.
Young_A Son
|
|
Dr.
Rares Scurtu
|
Prof.
Tae-Young Kim
|
|
Dr.
Dascalu Myrella Izabella
|
|
PROJECT
GENERAL OBJECTIVE
Science
is probably one of the first trades globalized over the world.
Regardless of nationality, scientists can make cooperative work
successfully based on their common research interests and
complementary expertise. The so-called ‘mobility’ program
can be a good example. In this direction, our general aim may be
described into one goal: to develop the effective research network
between Korea and Romania. We believe that broad visions for
constructing the bilateral research networking would be one of the
main keys to the success of this KICOS/ANCS research program.
Contrary
to other groups, our participating teams in Keimyung University,
Korea, and Institute of Physical Chemistry, Romania, have the
relatively long history of mutual relationships. In fact, two
research groups between Prof. Suh and Dr. Chihaia have started their
exchanging activities over the last decade since 1999. The
implementation of a Blade Cluster in the Institute of Physical
Chemistry, within the frame of the project CAPACITATI PNI-II
84/2007 founded by ANCS, is an important result of
the two groups collaboration, were Prof. Suh helped the Romanian
group with his knowledge about High Performance Computation
Centers.
Furthermore,
starting form 2005, we have organized and served as the
representative committee members for the
Korea/Romania Joint Workshop: Molecular Science and Engineering,
which has been held
every odd-year in Korea and even-year in Romania, respectively. This
workshop endeavors to
provide an effective bilateral forum between Korea and Romania in the
areas of chemistry, physics, molecular science,
and its related
engineering. In addition to the
Korea/Romania collaborations, we are currently conducting cooperative
research work with other EU countries including Spain, German,
Hungary, and Bulgaria. We are also aiming to creating the EU-FP7
research project throughout our successful research partnerships to
be made in this program.
PROJECT
DESCRIPTION
Soft
materials are materials with physical states that are characterized
by an energy scale comparable with room temperature thermal energy.
In spite of the various forms of these materials (liquids, colloids,
surfactants, polymers, foams, gels, microemulsions, granular
materials, membranes and some of biological materials), many of their
properties have common physicochemical origins, such as a large
number of internal degrees of freedom, weak interactions between
structural elements, and a delicate balance between entropic and
enthalpic contributions to the free energy. Such systems have a
complex structure that is difficult to be described directly from its
atomic or molecular consituents. The constituent mesoscopic
particles, may contain thousands or even millions of atoms,
interconnected to one another in complicated ways. These systems
self-organizes very often into mesoscopic physical structures (with
typical sizes 1 nm-1m) that are
much larger than the microscopic scale, and yet are much
smaller than the macroscopic (overall) scale of the material. They
come in a variety of forms, such as linear chain, branched,
star-shaped, dendritic, and copolymer, as well as taking on a variety
of functions, e.g., as steric stabilizers, additives, and depletants.
Additional flexibility arises from it being possible to influence the
structural and phase behaviour of polymer solutions by changing the
solvent quality.
The
properties and interactions of these mesoscopic structures may
determine the macroscopic behavior of the material. Their high
flexibility constitutes a major advantage of soft-matter systems in
comparison to their atomic counterparts is that one can engineer the
constituent particles at the molecular level. In this way, an
enormous variety of architectures can be achieved, leading to a
corresponding richness in the structural and phase behavior of such
systems. Typically, soft materials have weak interactions among
molecular or supramolecular components and are often either amorphous
or can self-assemble
from the liquid state. There are often many levels of complexity with
heirarchical, supramolecular structures that can be cooperative and
far from equilibrium.
Because
computational modeling and simulations are not constrained by the
current limit of our ability to fabricate the specific
nanostructures, it can explore and examine the potential targets for
the design and construction of a wide range of atomically defined
nanostructures, which can be a fundamental goal for nanotechnology.
The underlying theme in this project is to develop molecular
simulation approaches which accurately describe nanostructured pore
systems of interest. We will employ various molecular simulation
methods together with statistical thermodynamic approaches to
determine the detailed molecular properties, which are often
difficult or impossible to measure experimentally. Comparison with
experimental data can be used to investigate model nanopore systems,
and the ultimate goal is to use molecular simulations to carry out
experiments that cannot be undertaken in the real laboratory.
We
are most often concerned with the structural arrangments,
viscoelastic rheology, and/or mechanical behavior of these materials.
The properties of such materials may be diferent when they are
confined inside cavities or porous materials and this is our main
target of the present project to find informations about the soft
materials inside nanoporous sistems. The experimental investigation
of such confined sistems is dificult. Computer simulations have also
played a very important role in understanding the conformations of
confined mesoscopic particles, where the role of short-range
attractions appears to play a minor role in the overall behavior of
the macroscopic systems. The investigation asisted by computer
numerical simulations of the phenomena and the characterization of
the properties of the soft materials inside nanoporous sistems is the
main goal of our project. For
the various mesoscopic particles architectures the effective
interactions between suitably chosen coordinates are shown to be
ultrasoft, i.e., they either remain finite or diverge very slowly at
zero separation. As a consequence, the fluid phases have unusual
characteristics, including anomalous pair correlations and mean-field
like thermodynamic behaviour.
From
this point of view, as an intermediate between theory and experiment,
the equilibrium and transport properties obtained from molecular
simulations for confined penetrable fluids can provide an invaluable
tool against statistical thermodynamic approximations in the
literature. We will also focus on the development of algorithms and
computing methods for the structural characterization of a given
system based on the interatomic connectivity, e.g., clustering,
layering, ring-shaped topology, cage/channel formation, etc. Besides
such structural criteria, another methodological attention will be
given to the algorithm development for the characterization of
dynamic properties. A special atention will be payd to the topologic
characterization of the hydrogen bonded large periodic systems.
The
equilibrium and transport properties of soft-condensed systems via
Monte Carlo and molecular dynamics simulations will be important for
the molecular design of nanoporous materials and applications with an
aid of molecular-based computer simulations. In addition to such
classical computations, specific model potentials employed for
nanoporous systems will be parameterized by comparing the
experimental data with the simulation data obtained from
semiempirical and ab-initio quantum calculations.
Nanoscience and
nanoengineering can be the dominant direction for cutting-edge
technologies in this new century. In this field of nanotechnology, it
often requires research collaborations on the part of many
specialists to gain detailed perspective approaches, just as fashion
designers rely on weavers, tailors, and cutters to accomplish new
designs. It is therefore desirable to promote bilateral research work
to reach optimal solutions for nanotechnology. This situation will
open the possibility for interconnections between various topics in
nanotechnology to bring about new chances for further applications.
Prof.
Soong-Hyuck Suh’s research interests are associated with
statistical mechanical theories and molecular-based computer
simulations, with particular emphasis on the equilibrium and
transport properties of fluids and mixtures confined within model
nanopore systems. His work in this project is a continuation of his
current research work on model nanopore systems at the atomic and
molecular level, where theoretical and computational approaches have
demonstrated that such a route to molecular science and engineering
is quite viable. Research areas in this direction can open the way to
the effective design and the improved fabrication for nanoporous and
nanocomposite materials to be used in advanced nanotechnologies. He
implemented ultrasoft and bounded potentials in a simulation code
developed in his laboratory, enabling the users to increase the
complexity of systems that can be modeled in the fields of
nanomaterials, molecular crystals, polymers and organic chemistry.
His software provides a coarse-grained approach that allows the
combination of soft and hard materials in a single calculation.
Dr.
Chihaia has developed various computational algorithms. His studies
in this direction include the rigid-body dynamics, the optimal
searching routine of rings and cages with arbitrary size based on the
atom-to-atom connectivity, the hydrogen bond topology, and the
automatic building of the potential energy surface for the adsorption
and diffusion phenomena. Recently, he has initiated and pioneered the
research project related to the high computing system in Romania,
entitled as the High Performance Computer Cluster for Computational
Material Science in Romania. He has experiences on both the quantum
and the classical molecular simulations, e.g., the adsorption and
diffusion of molecules and small clusters on various surfaces, the
characterization of the structural and dynamic features of the
channel- and cage-like compounds (carbon nanotube, porous silicon,
buckyball, water clusters and clathrate hydrates) using quantum
chemistry and solid states physics, and the embedding methods for the
extended atomic and molecular systems.
The
two groups are complementing each other by their abilities, knowldges
and their infrastuctures. The results of their collaboration
demonstrate the efficiency of their work together. Both
countries of Korea and Romania, based on our experience of previous
research cooperation, have their own strength and advantage: the
fundamental science to the Romanian side and the engineering
application to the Korean side. In order to be globally competitive,
it need to have feedbacks and interactions among scientists and
engineers in both countries. Theoretical and computational methods to
be investigated in this work will play a leading role in the
development of nanosystems, guiding the fundamental issues in
molecular design and modeling.
REZULTS
To
test the installation codes so we chose the system soft materials
(soft materials) that are material physical state characterized by
energy with corresponding heat values close to room
temperature. Despite various forms of these materials (liquids,
colloids, surfactants, polymers, foams, gels, microemulsions,
granular materials, membranes and some biological matriale) many of
their properties have common physicochemical origins, such as a large
number of degrees of freedom, weak interactions between structural
elements and a delicate balance between entropy and enthalpy
contributions to their free energy. Such systems have a complex
structure difficult to describe directly the atomic or molecular
their constituents. Constituent particles may contain thousands and
even millions of atoms, interconnected in a complicated way. These
systems self-organize into mesoscopic physical structures (typical
size between 1 nm to 1μm) are higher as microscopic scale but much
smaller than macroscopic scale the material. These meso-objects have
various forms such as linear strings, branched type star, and
dendritic copolymers. They have a variety of functions such as steric
stabilizers, additives and dispersion.
Their flexibility
can influence the structure and polymer solutions comporatarea by
changing the solvent quality. Structural properties and interactions
of these can cause mesoscopic macroscopic behavior of the material.
Their high flexibility is an advantage compared to their opponents
because they allow manipulation of their atomic constituent particles
at the molecular level. This can get a wide variety of architectures,
with different behaviors.
We list some examples of soft materials:
liquids, colloids, polymers, foams, gels, granular materials as well
as more complex systems such as bacterial suspensions and biological
polymers. Usually soft materials have weak interactions between
molecular or supramolecular components and are usually amorphous form
or may be self-assembled from licide states. Often these materials
has many levels of complexity with hierarchical supramolecular
structures that can be competitive in states far from equilibrium. Of
great interest to our teams surfactant systems, particularly those
formed by sodium sulfate. Sodium dodecyl sulfate (SDS - Sodium
Sulfate DODECYL) is an anionic detergent and distorting proteins that
confer a negative electrical charge SDS-protein complex, which allows
us to control migration of protein molecular function of their mass
and their electrical charge. It is very useful in separating
nano-objects such as graphene, nanotubes or fullerenes and
nano-systems formation control and meso-porous. Below we present
results obtained in model systems containing it some water solutions
- SDS.
Sodium dodecyl
sulphate - SDS
Sodium dodecyl
sulfate is an organic compound with the formula NaC12H25SO4 or CH3
(CH2) 11OSO3Na, consisting of a chain of 12 carbon atoms attached to
a sulfate group SO3 through one of oxygen. It is an anionic
surfactant. To characterize the energy stability of this system, we
performed DFT calculations using quantum type and exchange
correlation potential PW91 GGA type and a numerical DNP basis.
Conditions for achieving convergence were very strict geometric
optimization: 10-6 Ha energy, energy gradient 10-3 Ha / A, 0.005 A.
The energy shift of about sodium atom chain of CH3 (CH2) 11OSO3 is
given by relationship
BE (Na) = E (CH3
(CH2) 11OSO3Na) - [E (CH3 (CH2) 11OSO3-) + E (Na +)]
where E (CH3 (CH2)
11OSO3Na) is the energy of the whole system, E (CH3 (CH2) 11OSO3-) is
the energy chain CH3 (CH2) 11OSO3-and E (Na +) is the energy of ion
sodium alone (104 015 kcal / mol). The most stable conformers of CH3
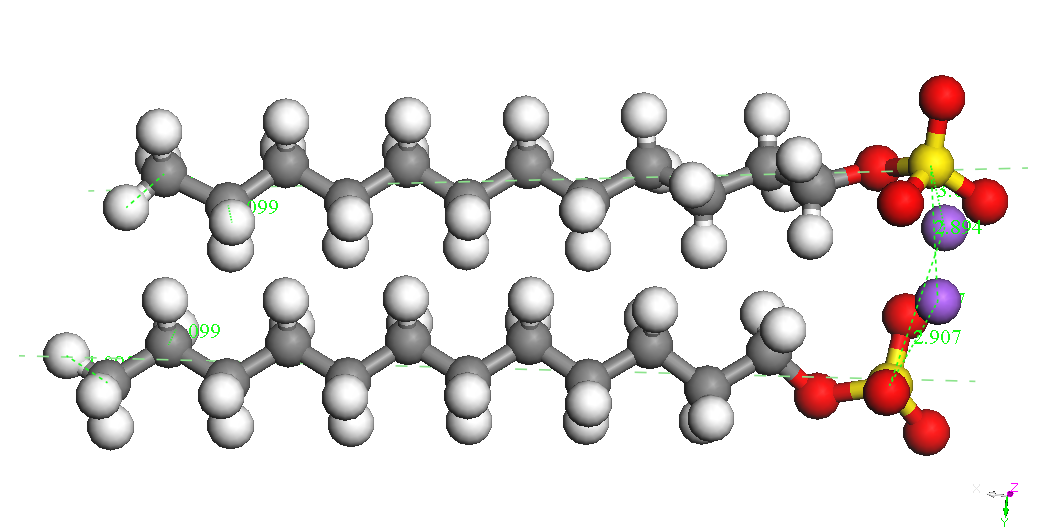
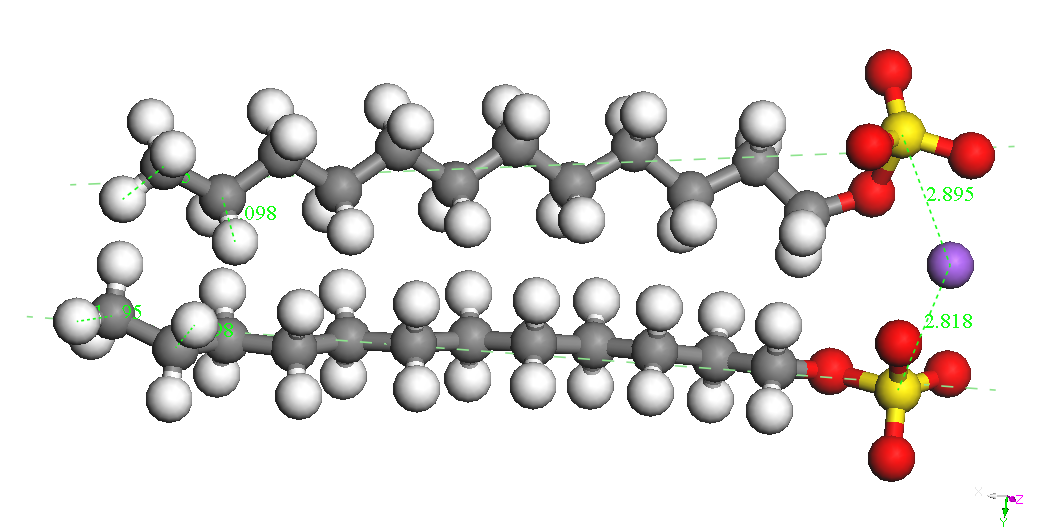
(CH2) 11OSO3-is presented in Table 1. Sodium ion binds to the sulfate
group in various positions at a distance S-Na of about 2.72 A. The
most stable conformers is called CH3 (CH2) 11OSO3Na, Na - down in
Table 1.
Table 1. Various
associated structures and their energies SDS system connectors (BE).
|
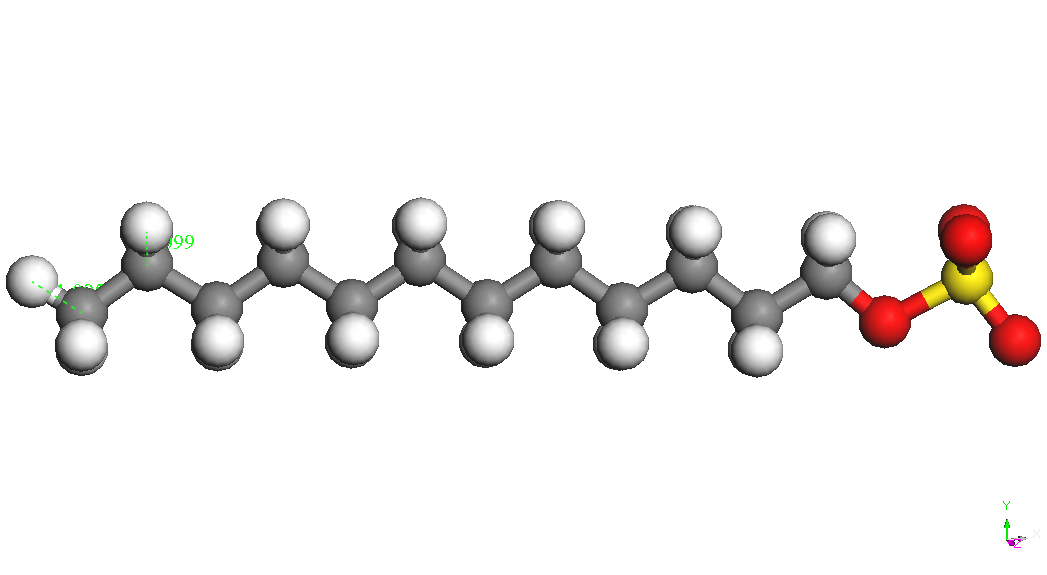
|
[CH3(CH2)11OSO3]-
BE
= -4322.832kcal/mol
|
|
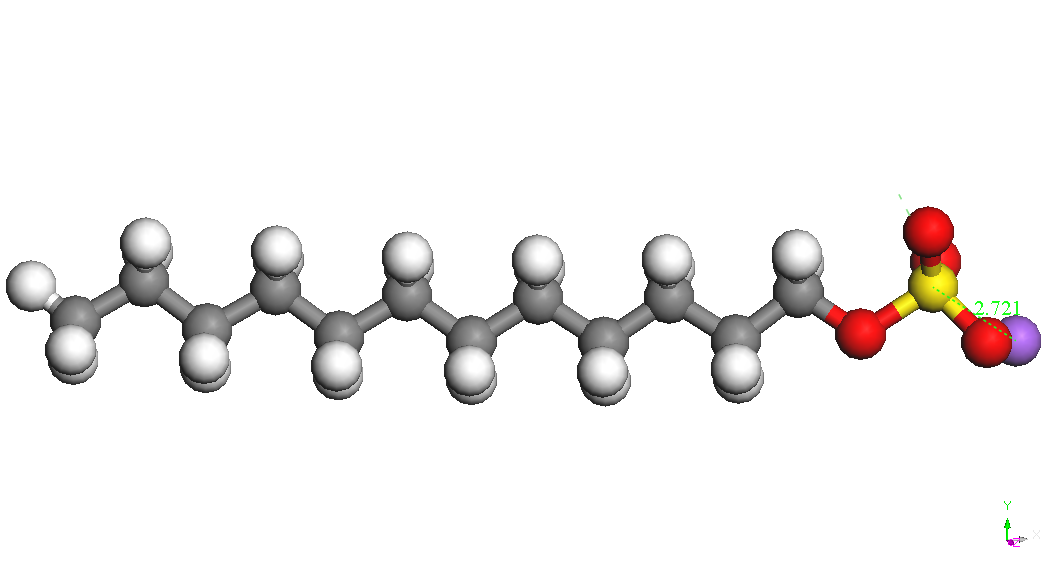
|
CH3(CH2)11OSO3Na,
Na – down (twisted)
BE
= -4337.834 kcal/mol
BE(Na)
= -74.177 kcal/mol
|
|
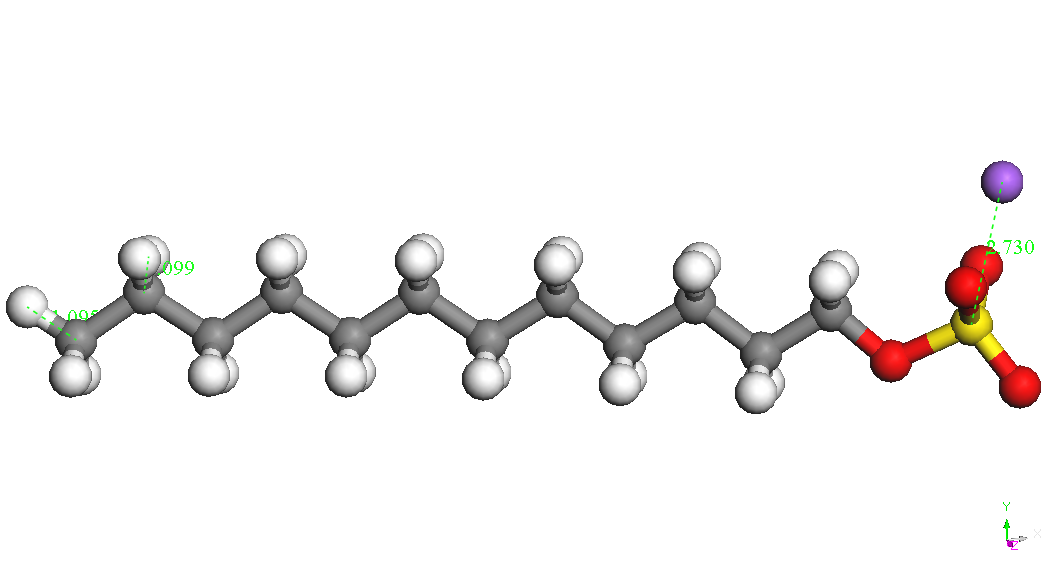
|
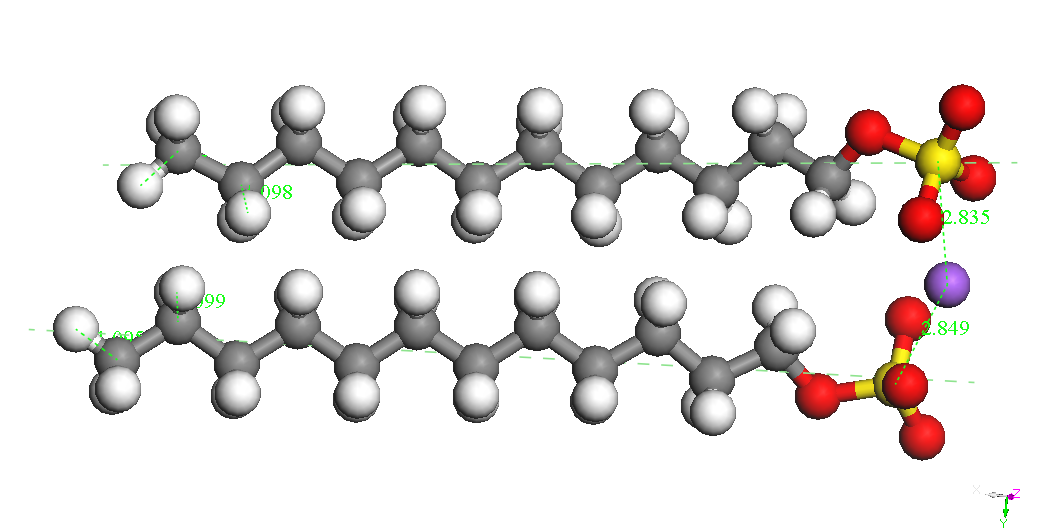
CH3(CH2)11OSO3Na
, Na – up
BE
= -4336.335 kcal/mol
BE(Na)
= -72.678 kcal/mol
|
|
|
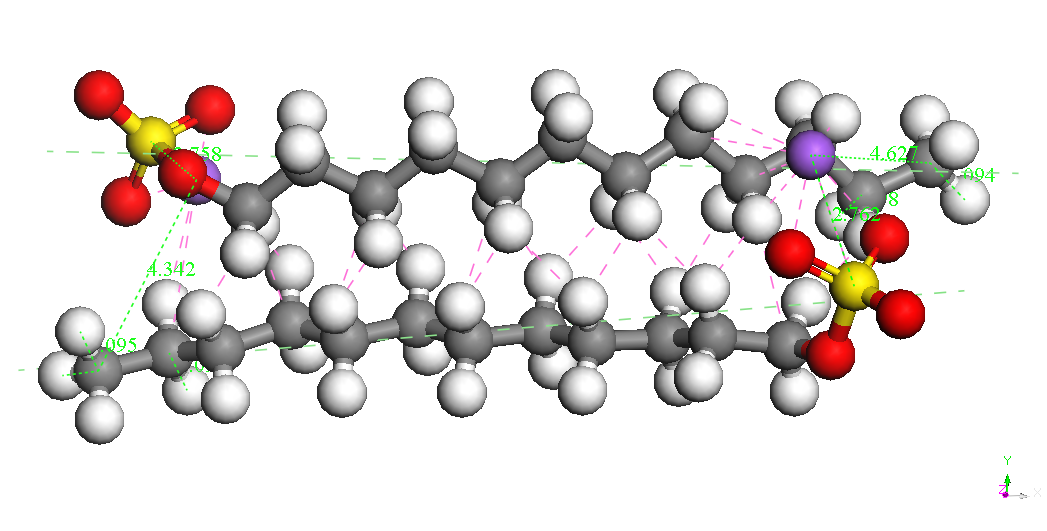
Dimer
Head-Head Parallel 1
BE
= -8743.650 kcal/mol
|
|
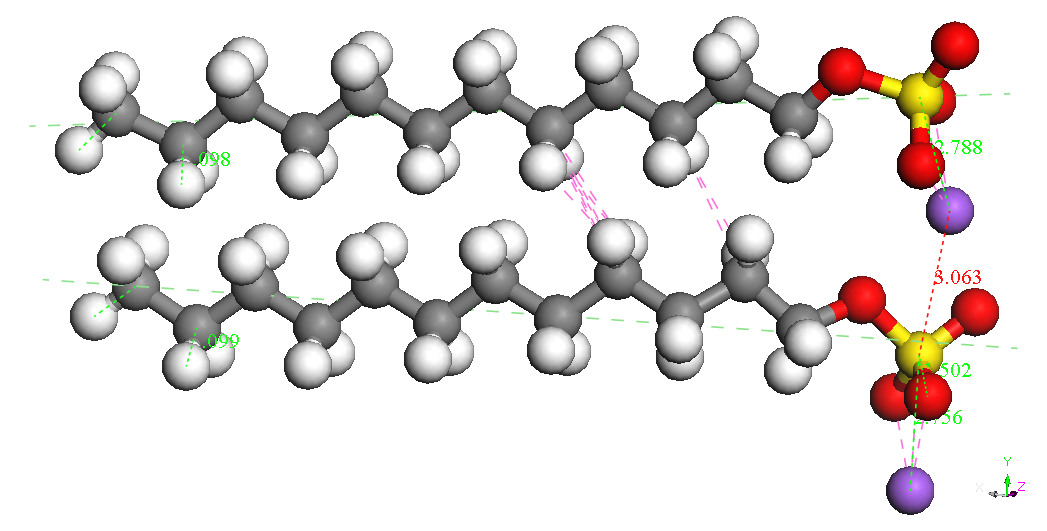
|
Dimer
Head-Head Parallel 2
BE
= -8730.682kcal/mol
|
|
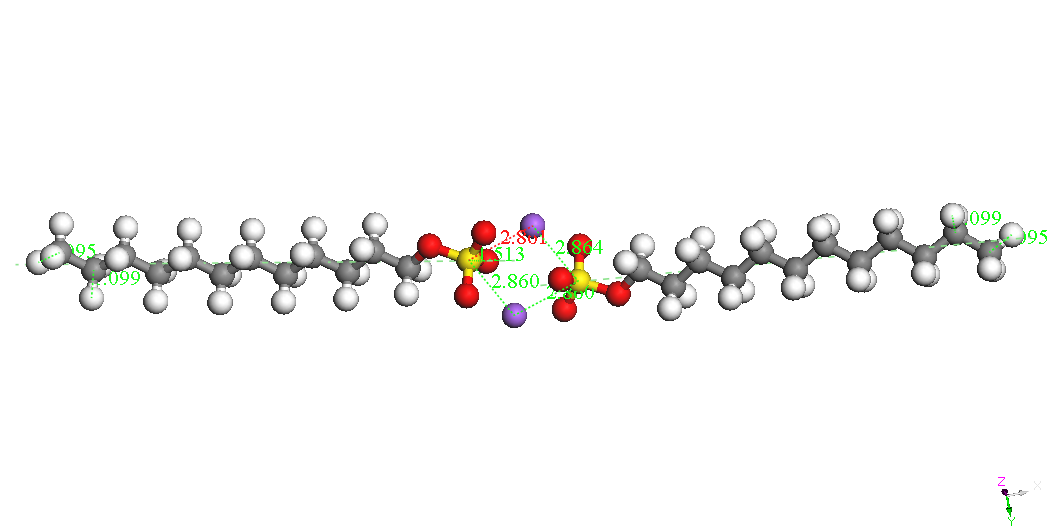
|
Dimer
Head-Head Along
BE
= -8715.747kcal/mol
|
|
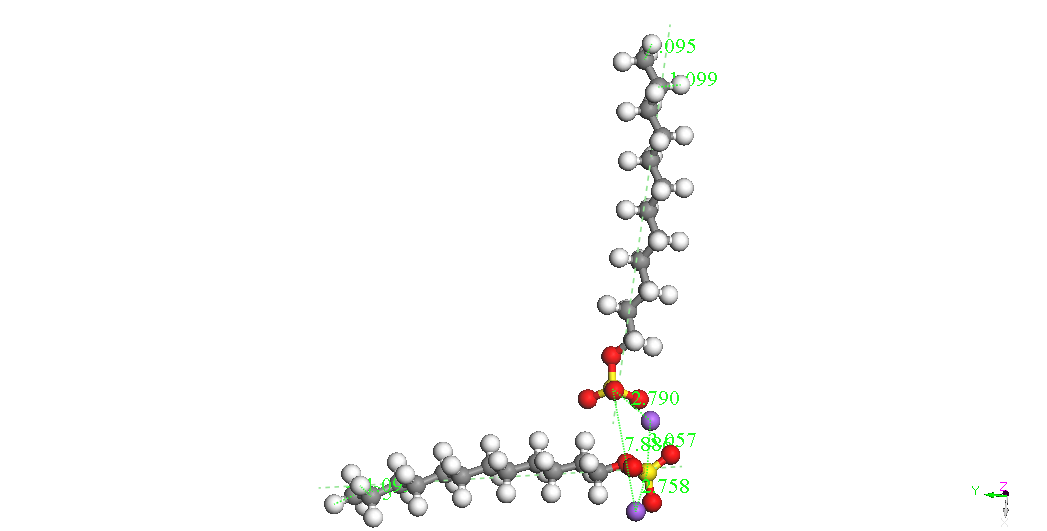
|
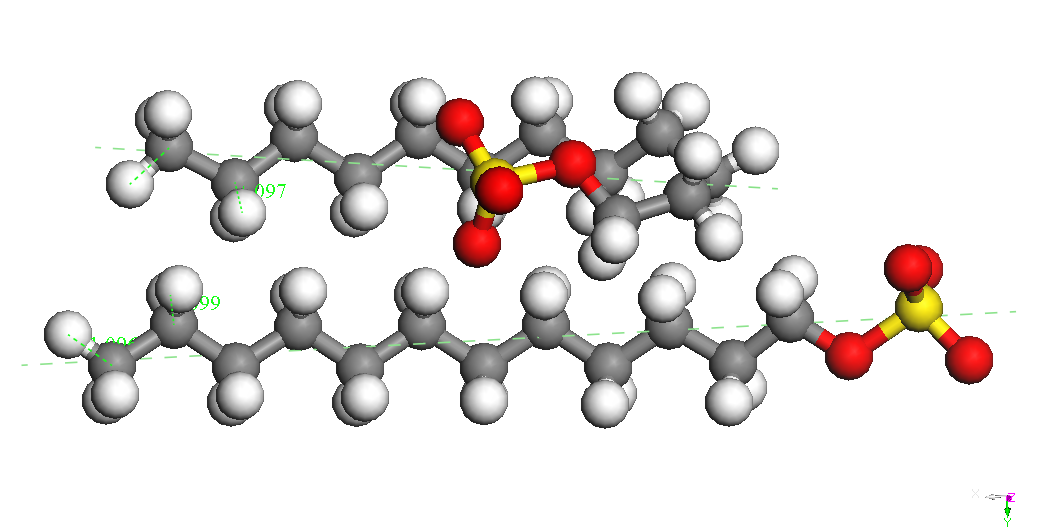
Dimer
Head-Head perpendicular
BE
= -8697.493kcal/mol
|
|
|
Dimer-Na
Head-Head Parallel 2
BE
= -8744.893kcal/mol
|
|
|
Dimer-Na
Head-Head Parallel 1
BE
= -8735.920 kcal/mol
|
|
|
Dimer-Na
Teil-Head Parallel
BE
= -8721.021 kcal/mol
|
|
|
Dimer-2Na
Head-Head Parallel 2
BE
= -8670.233kcal/mol
|
If dimers isolated
can be seen as the most stable isomer is the called Dimer Head-Head
Parallel 1 for the two molecules SDS are parallel with the same
orientation and the two ions Na + are located on one side and the
other to two sulfate groups. It is possible that immersion in water
system to modify the polarization of SDS molecules which would affect
the stability of isomers but do not expect to change the location and
orientation of two molecules parallel. An abinitio study would be
very expensive due to the large number of molecules and
configurations that should be investigated. SDS molecules form
micelles that water to concentrations higher than a critical value
suggests a parallel arrangement of molecules preferentially SDS.
Coarse Grain
parameterization of force fields for SDS systems, water and
allotropic forms of carbon
Potential energy
surface for fields of type d effort coarse grain is much smoother
than those of all-atoms (AA). The main requirement of these fields is
to reproduce the overall movement of atomic groups that are
represented by pseudoparticulele beads. CG potential is usually
parameterized to reproduce the radial distribution function of
different pairs of elements in the system or by reversing the
equation molecular dynamics simulations Boltzann of AA. Therefore
these potential parameters depend on the molecular dynamics
simulations run all-atoms including the time step used for
integrating the equation of motion and system temperature. CGMD
simulation time step can be considered for 5 to 20 times higher than
that used for AA simulations, allowing the study of phenomena that
occur at larger time scales. Also reduces the number of particles
between the forces of interaction is calculated and whose equation of
motion is integrated. Thus the calculation effort is much reduced,
allowing the study of larger systems and larger stroke. On the other
hand, CG forces and potentials have mathematical forms simpler,
generally short distance, usually because the potentials are
truncated. A class of potential high-use is the potential to
parameterization Martini.
These
potential interactions consist of connection type, usually with a
quadratic form of the difference distance between two particles and
the value of the equilibrium distance and interactions of nelegatura,
usually represented by Lennard-Jonnes potential truncated. In this
study we have taken from literature force field parameters of type GC
Martini 2.0 [SJ Marrink, H.J. Risselada, S. Yefimov, D.T. Tielman and
A.H. de Vries, J.Phys.Chem.B, 111, 2007, 7812] and I used to
interesting systems after a consistency check parameters. Thus we
performed molecular dynamics calculations of GC systems in Table 2.
The potential Martini four water molecules are represented by a
single particle pseudo-P4, the SDS molecule a fragment of four
carbons and 4 or 5 hydrogen is represented by a particle C2,
SO4-sulfate group is represented by a particle Qa charged -1, and
sodium ion by a charged particle Qd; in carbon systems, two linked
carbon atoms are represented by a particle sc4. For GC systems of
water tend to freeze at room temperature, we replaced BP4 particles
between 5 and 10% of P4 particles. They are designed to disrupt the
arrangement of water molecules in ordered structures and
prevent,''freezing system.
We built two amorphous systems
consisting of water and SDS a total of 20 000 molecules in
representing AA and carbon systems presented in Table 2. I turned AA
systems in CG equivalent systems by replacing groups of atoms with
their corspondentii CG. To reduce internal tensions have optimized CG
structures mantinand first fixed shape and size of cells and then I
completely relaxed systems. Simulations were performed in NVT
thermodynamic ensembles for a temperature of 300 K, maintained by a
Nose thermostat with a parameter Q = 100. They tried different time
steps, the optimal for all systems is 25 fs, which is an increase in
the time scale of about 50 times the AA simulations. Systems were
balanced for 20 ns and thermodynamic values were
averaged from the other 10 ns. The results were compared with those
obtained from AA simulations for a time step of 0.5 fs for a period
of equilibration of 200 ps. To see a satisfactory reproduction of
radial distribution functions. Simulations were repeated for NPT
ensembles, under a pressure of 1 atm using a barometer Berensen.
Simualrile network constants obtained in AA are reproduced in a 5%
margin of error in CG computations.
Table
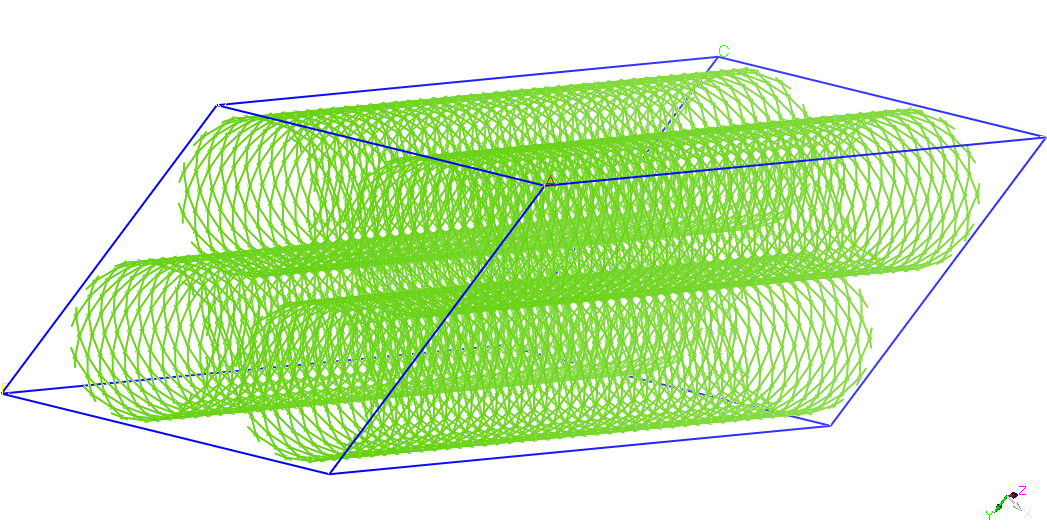
2. CG representation of the atomic systems of interest in this study
|
System
|
Atomistic
Representation
Constituent
Elements – Atoms
|
Coarse
Grained Representation
Constituent
Elements – Beads
|
|
4
water molecules
|
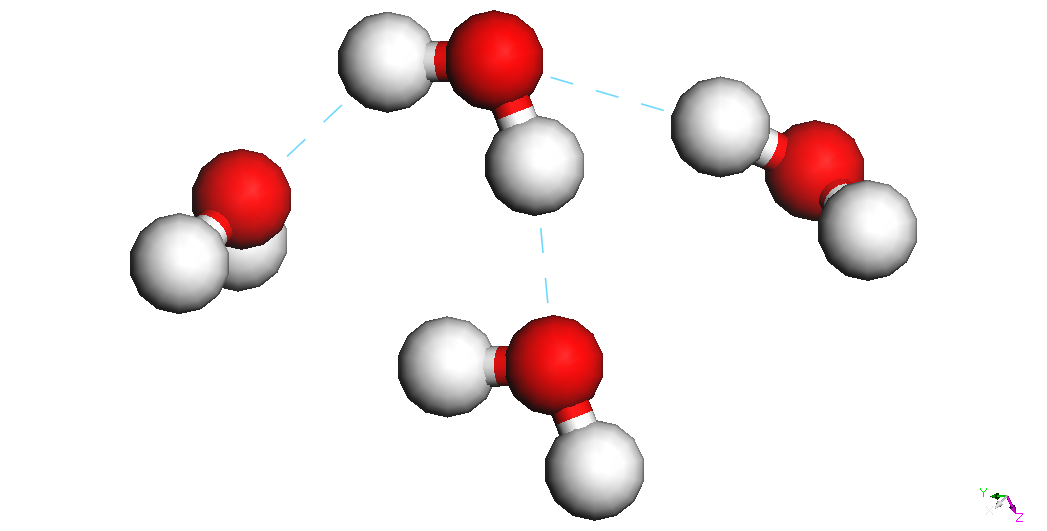
|

|
|
SDS
|
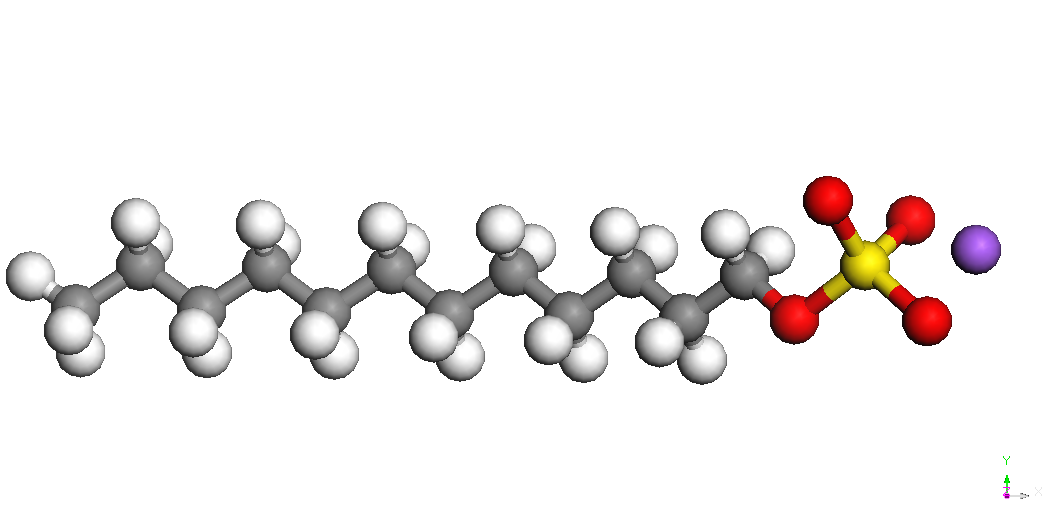
|
|
|
CNT
(12,12)
|
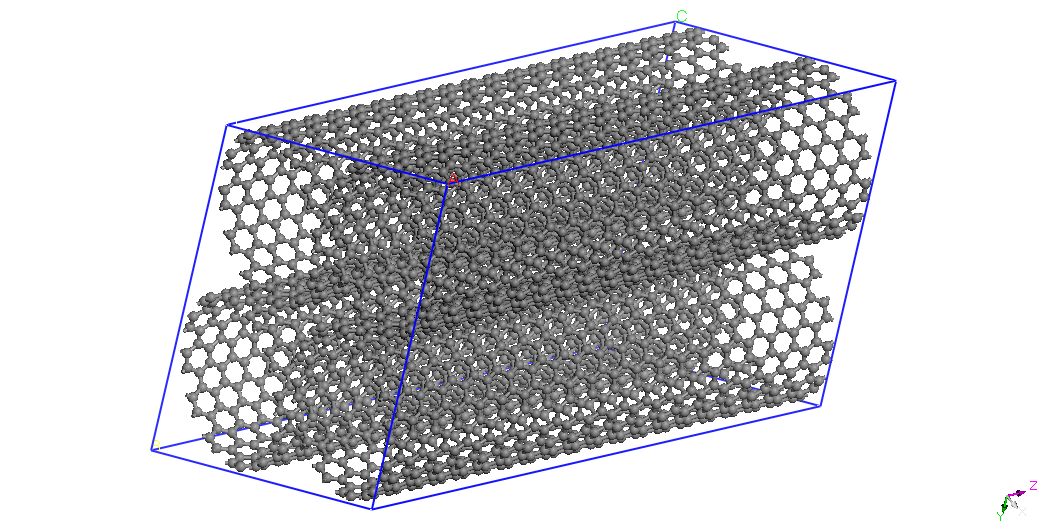
|
|
|
Amorph
Carbon
|

|

|
SDS micelles
immersed in water
I
checked reproduction density values of pure water and water-SDS
solution by molecular dynamics simulations for 20 ns GC, using a
statistical ensemble under the NPT (T = 300K, P = 1 atm, Berendsen
barostat). Initial system density was 2 g/cm3 and or obtained after a
period of 500 ps equilibrium densities of 1 to 2 g/cm3. In water-SDS
solution of SDS molecules form agglomerations in which the molecules
are oriented with sodium ions in the direction changed in comparison.
From other studies in literature show that for more than a critical
value of SDS concentration, these molecules are quasi-spherical
clusters gather the SDS molecules are aligned radial ends where ions
Na + are present, outside clusters. These clusters are stable over
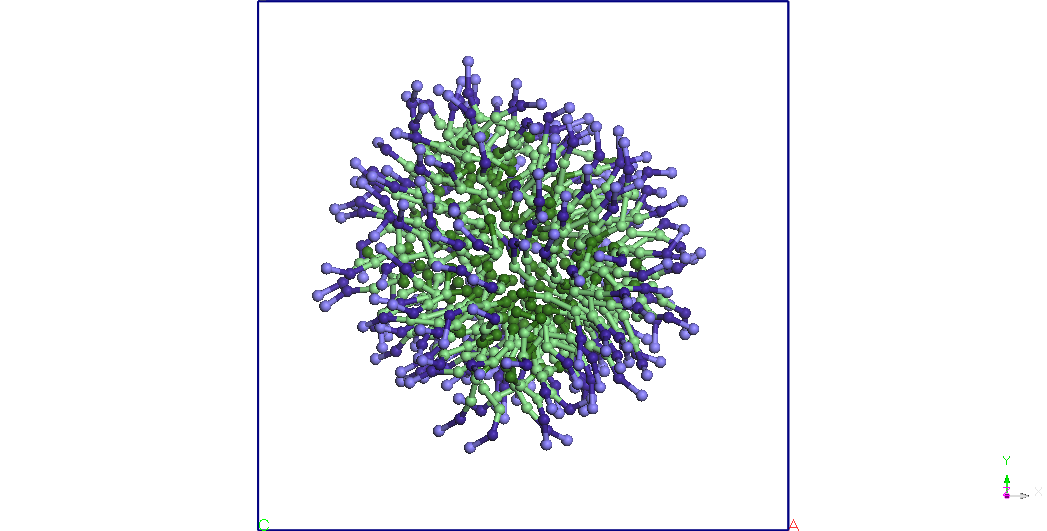
time and are in fact micelles.
|
Water
equilibrium
density 1.0 g/cm3
|

|
|
SDS
- water solution
initial
structure
|

|
|
final
structure, density 0.8 g/cm3
|

|
Figure 2. Systems
used in the study of reproductive density of pure water and water-SDS
solution.
|
0
ns
|
|
|
50
ns
|

|
Figure 3. The
structure of micelles of SDS immersed in water. Pentriu clarity water
molecules are not represented.
For
a sodium concentration of 2 to 3 molecules of water molecules have
formed a stable Miceli remains almost spherical after 50 ns of
simulation for a CG NVT thermodynamic ensemble. T = 300K (see Figure
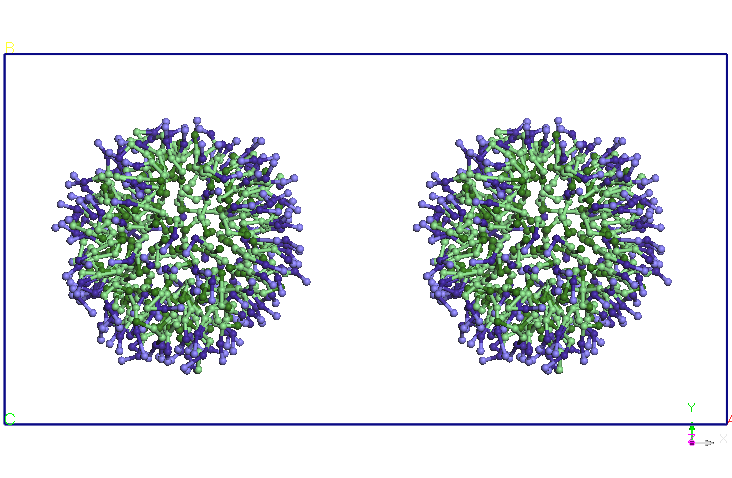
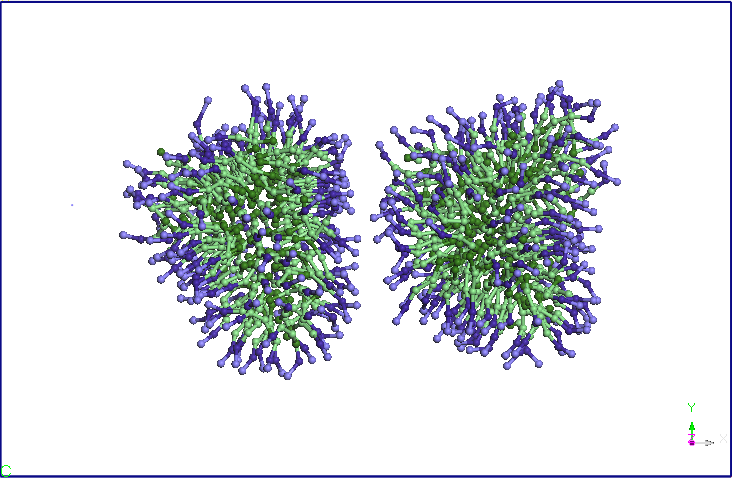
3). Using the balanced structure we have built with double SDS Miceli
a dimer structure Miceli-SDS. Initial distance between the centers of
gravity of the two micelles is 8.46 nm. I relaxed for 1ns system thus
formed a NPT ensemble (T = 300K, P = 1 atm, Berendsen barostat). Note
that at the end of the simulation the two micelles is close to an
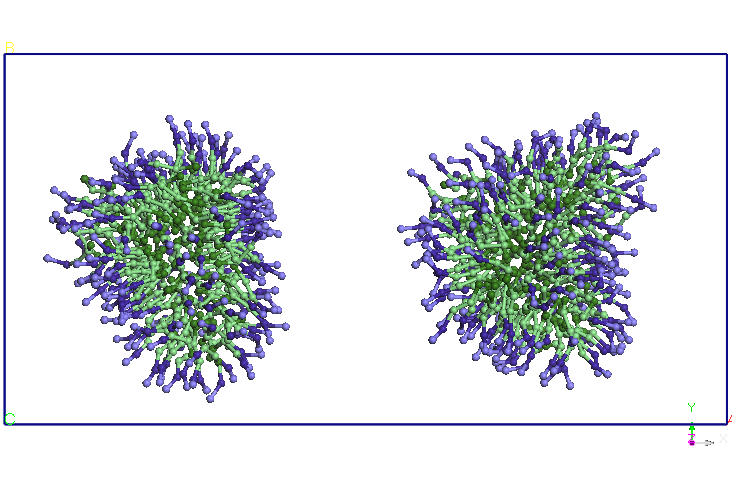
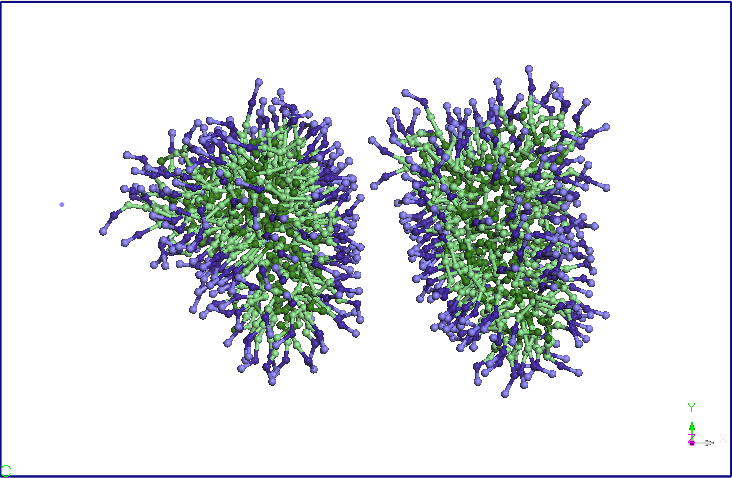
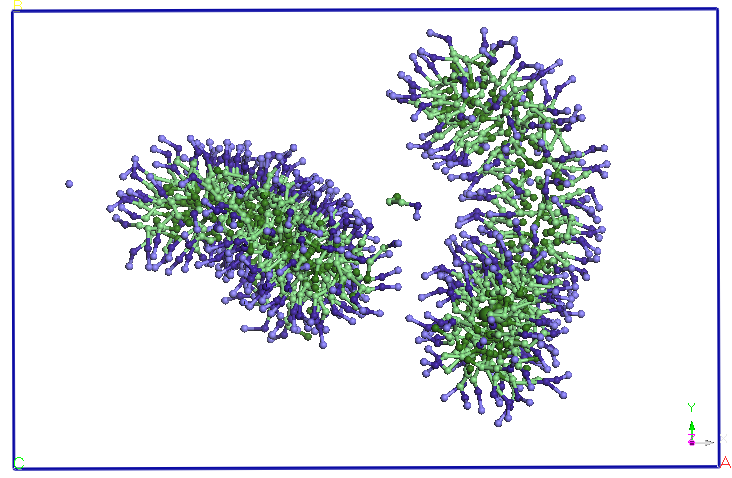
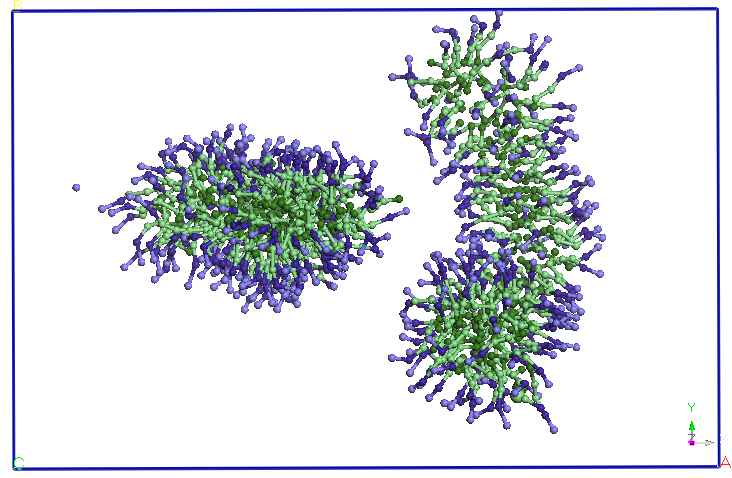
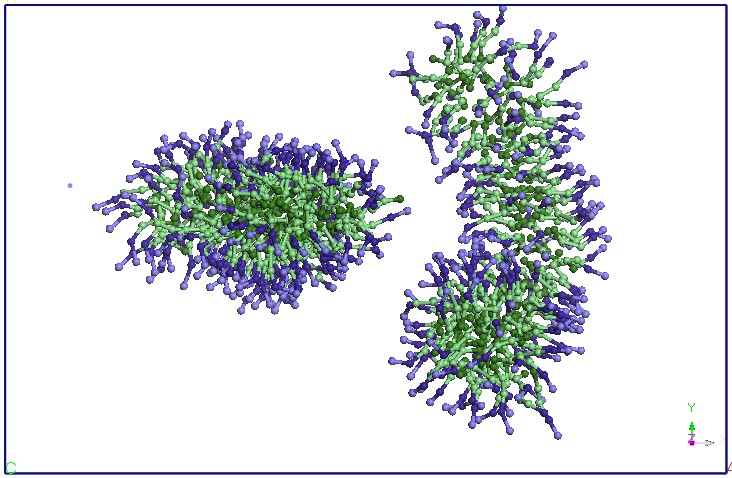
average distance of 5.60 nm (see Figure 4). The two micelles change
their shape slightly, initially spherical. We continued the
simulation in NVT ensemble by fixing the size of simulation box
obtained in NPT simulations and keeping the other conditions of
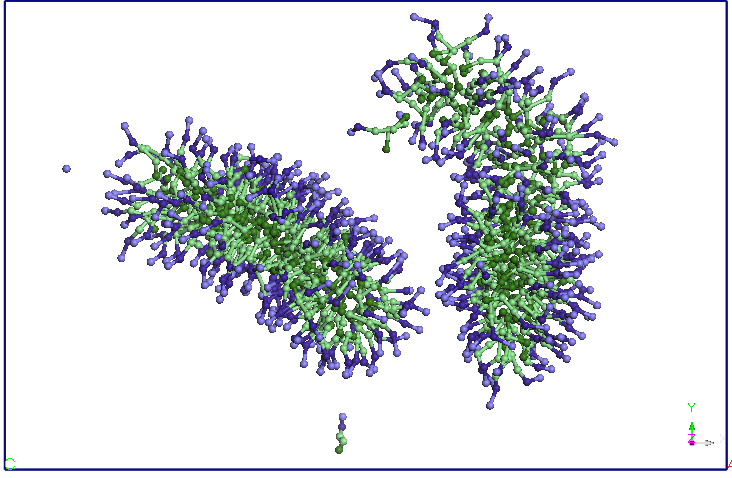
previous CG simuarii. Note that after 5ns micelles elongate and
two-and change the orientation, approaching the two ends. After about
9.5 ns distance between the two endings is reduced and more SDS
molecules and diffusion occurs from Miceli to another. A migration of
molecules from these SDS micelles one of two in favor downsize their
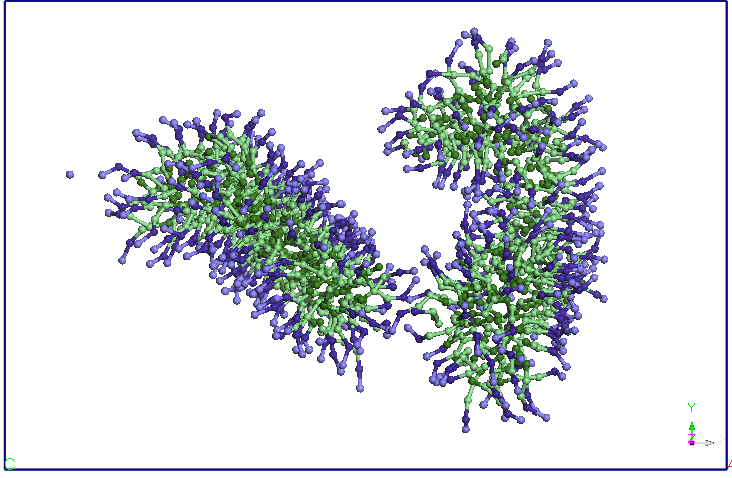
other micelles (after about 15 ns). After 25 ns, no diffusion is
observed between the two molecules SDS micelles. The two micelles
holds its shape and orientation of the end of the 40 ns simulation.
It is important to mention that during these simulations SDS
molecules retains most of the time orienttarea with hydrophilic end
(Na +) outward toward the water.
|
|
|
|
|
0
ps / NPT
|
100
ps / NPT
|
1
ns / NPT
|
|
|
|
|
|
2
ns / NVT
|
5
ns / NVT
|
10
ns / NVT
|
|
|
|
|
|
15
ns / NVT
|
25
ns / NVT
|
40
ns / NVT
|
Figure 4. Evolution
of two micelles system immersed in water in molecular dynamics
simulations in NPT and NVT thermodynamic ensembles. Pentriu clarity
water molecules are not represented.
Diffusion
through amorphous nanoporous carbon
Sieves with
nanometer size windows are very important in selectivity and
production of ordered systems, playing in their preparation mask. We
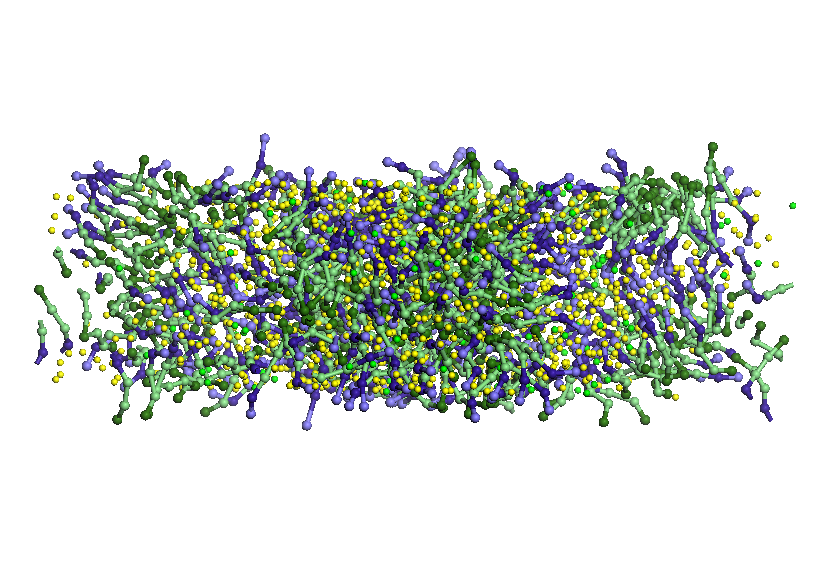
assembled in the same cell of two layers of graphene simulation, a
layer of water-SDS solution and an amorphous carbon mesh windows /
average pore size of 13 A (see Figure 5). The three systems are
balanced separately by CG molecular dynamics simulations at a
temperature of 300 K and amorphous carbon graphene layers are
separated by empty space. Graphene layers are designed to separate
water-SDS solution and any water molecules and SDS would migrate
through porous carbon windows.
|

|

|

|
|

|
|

|
|
Two
layers of graphene
|
SDS
- water solution
|
Amorphous
carbon nanosieve
|
Figure
5. Images from top and front of the system components investigated.
Figure 6. Evolution
of the system during molecular dynamics simulations, in terms of
imposing rigid porous system uniui for average pore size of 13 A.
To
see the role played by rigid carbon structures we performed two
simulations: i) maintaining fixed positions pseud, carbon particles
and ii) letting them move freely according to Newton dynamics. Both
simulations Sund NVT thermodynamic ensembles performed by keeping
fixed the basic cell and temperature T = 300K, controlled with a Nose
thermostat with parameter Q = 100. While maintaining a fixed
pseudo-particles of carbon is found that during the first 50 ps, the
water-SDS solution, stick 'porous carbon and a few water molecules
penetrate inside windows and SDS (see Figure 6) and remain localized
there throughout the simulation (50ns). Only a few water molecules
get in the free zone, no SDS molecule but not fall in this area.
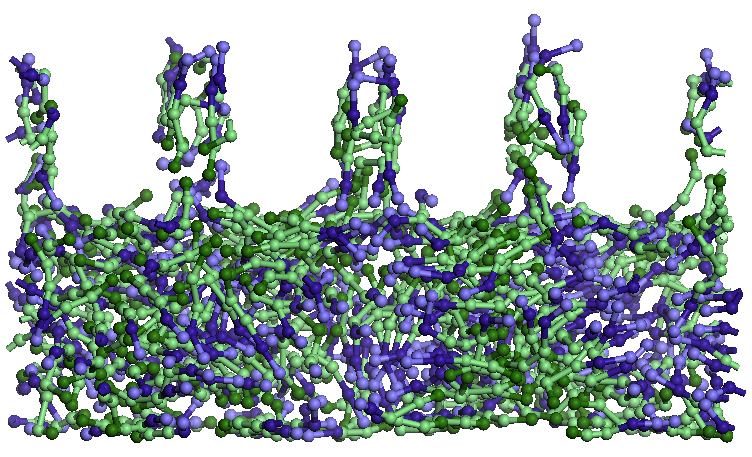
Figure
7. Details of the structures formed by water molecules (green spheres
isolated) and SDS (chains, in which sodium ions are blue heads)
located near the amorphous carbon (left) and that adsorbed on the top
layer of graphene (right).
Upper
graphene surface a small number of SDS molecules adsorb water and
forming a layer. SDS molecules adsorb parallel to the layer of
graphene, a single molecule is perpendicular to the layer. Some water
molecules enter and leave the pores SDS or change their orientation.
Pore size is large enough to access 4-5 SDS molecules
and several water molecules. Water molecules are forced to leave
shortly pores (1-2 ps) after they penetrate. SDS molecules that
penetrate the pores have a hydrophilic end orientation to the top of
the pores, leaving the hydrophobic end-oriented solution. Water-SDS
solution layer changes its original structure by rearranging SDS
molecules in solution: molecules in the pores are oriented vertically
with hydrophobic end to the pore, in the vicinity of the hydrophobic
ends of SDS molecules entering the pores and the remaining SDS
molecules orienteza hydrophobic ends hydrophilic ends of SDS
molecules to close pores. SDS molecules in the lower layer solution
is oriented almost horizontally oriented heads trying to take parts
of the same type. It is assumed that this restructuring in size,
shape and spacing of pores plays an important role as well as
temperature, thickness and concentration of SDS solution.
Figure 7. Evolution
of the system during molecular dynamics simulations, in terms of
imposing a porous flexible system for average pore size of 13 A.
If full
flexibilisation carbon structures in the first 50 ps the system
evolution is very similar to the case of simulation with rigid carbon
structures but another 10 ps after the two layers of graphite and
carbon curls porous due to vibrations extends vertically about 2-3%.
Within a few nanoseconds water-SDS solution is constrained between
the deoua carbon structures. Here there may be some artifacts in the
simulation regarding the initial conditions, ie random choice of
initial rates of carbon atoms can give these systems the rotation
movements in all conditions, friction 'between the carbon layers
images to transform these movements internal vibration and rotation
here to have these excessive wane graphene layers. However, these
artifacts have no essential influence on molecules permeated into the
pores. SDS molecules permeated into the pores have the same
orientation as for the system with rigid carbon structures which
requires a similar behavior of water molecules in the SDS solution as
with the previous simulation.