Back to the basis!
Revisiting the Building Elements of Computational Chemistry.
Here we unravel heavy background preoccupations, worked already since several years which still need some more time to reach maturity for a market strike. As detailed, there are serious flaws in actual Gaussian-Type basis sets, deeper than usually known and considered as acceptable. In general, we are practicing quantum chemistry in non-routine manner, avoiding easy way of few-clicks-away results.
We hold a critical perspective on quantum calculations, preparing possible a revolutionary stand for the desiderata of a new generation of methods in applied theoretical chemistry, while still using the existing panoply of codes and controls in the well-tempered manner.
We would invite users and developers to meet at the frontier of their domains, communicating in the lingua franca of chemical intuition. A computer revolution that took away about two decades ago, democratized the access to hardware and software to a large publicum. So, not only large masses ended using all sorts of personal computing devices, but experimental peoples were able to approach user-friendly quantum codes to complement information from experiment. After all, the use of a graphical interface of a code is not much different from handling the panels of buttons of a spectrometer. However, the ultimate level of applying quantum chemistry in realistic manner was not yet been reached.
As the society in ensemble is preparing for a new wave and even a shock due to new informatic technologies, up to quantum computing and artificial intelligence, the question is how this could be reflected in computational chemistry.
We would "instigate" the mass of users and elites of developers to think of possible revolutions, at least as thought experiments.
As seeds of non-orthodox views, one may consider the following challenges. Is it the time to reconsider the actual domination of Gaussian Type Orbitals (GTOs) in quantum chemistry? With GTOs we are in a status-quo established in the decades of poor computer resources. But, it is no longer the case! Most of the users think that we can indulge the wrong behaviour of exp(-ar2) primitives near nucleus, while are not aware that GTOs can be malformed at long range. Well, this happens because of severe limitations in radial degrees of freedom. Thus, all s-type orbitals are made of only exp(-ar2) components, all p-type consist in only r*exp(-ar2), and so on. A given l quantum number is accounted only by rl*exp(-ar2) primitives, while a simple reasoning will say that an enlarged flexibility e.g. by rk*exp(-ar2), with k ranging from l to a maximal n-1 (related with higher attempted main quantum number n), would be a better practice, technically. The previously alleged drawback is reflected in bad account of atomic spectroscopy. We dare peoples to try to see how appallingly deficient the hydrogen excited states (2s, 3s orbital promotions) are accounted with actual GTOs. To the best of our knowledge, the limitations of GTOs due to their constrained design are also manifest in the simulation of chemical reactions of small molecules in gas phase, because the long-range orbital tails and atomic excited states are not appropriately simulated.
The following pictures are low-resolution excerpt of a material demonstrating first how appalingy bad GTOs are for the simplest atom, the hydrogen, proposing new principles. After that, partial results on heavier atoms are exemplified. We aim to chart completely the basis sets for the whole periodic table, as matter of a future project. The problem stays not only in producing the bases, a goal for which we are ready, but the fact that actual molecular GTO-based codes have an architecture critically tied to existing limited GTO formats. This means that drastic revision of whole inter-atomic integral packages (aside atomic bases) should be replaced, an overwhelming task. Of course, a great resistance against such painful modifications is expected. However, we continue our, for the moment silent endeavour, aiming for the great stakes.
Optimizing new Gaussian-type basis sets for the series of first light atoms.
As pointed previously, the nowadays quantum chemical is heavily based based on the so-called Gaussian Type Orbitals (GTOs).[1],[2] The radial form of an atomic GTO primitive, as function of radius r (i.e. the departure of the electron from the nucleus), depends on the parameter inside the exponential (z) and a certain factor as a power of radius, rk-1, ascribed as:
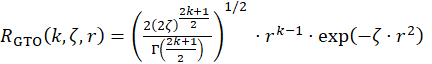(1)
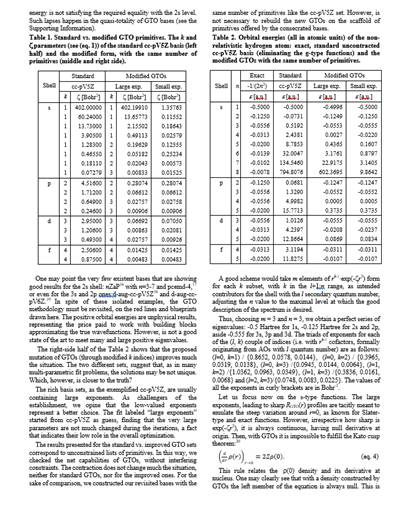
where G is the incomplete Gamma function.[3] There is a rich variety of GTOs, all undergoing a hidden drawback. The problem with the GTOs does not stay only in the exp(-zr2) part, as the quasi-totality of users (and even developers) seem to believe, but in a wrong design of the polynomial cofactors. Namely, for all the Gaussian basis sets in use the k factor in the above formula is strictly limited to the l+1 value with respect to the l quantum number specific to a shell (l=0, 1, 2 for respective s, p, d etc). In the previous stage we discussed in detail this aspect for the hydrogen atom. Now will advance toward the first elements of the periodic table. We propose a well-proportionated scheme taking m elements of rk-1*exp(-zr2) form for each k subset belonging to a l shell, with k in the l+1:n range, confining the n value to the maximal level for which the good description of the spectrum is desired.
Table 1. The fit of the
GTO 
functions for
second row of the periodic table. The first column contains the definition of
pre-exponential factors, the content of the table consisting in the 
exponential
parameters (in Bohr-2).
|
k |
Li |
Be |
B |
C |
N |
O |
F |
Ne |
|
|
s |
1 |
0.00221 |
0.01371 |
0.00401 |
0.07071 |
0.00540 |
0.00629 |
0.00727 |
0.00991 |
|
1 |
0.24895 |
1.07233 |
0.58312 |
3.94029 |
0.87066 |
1.07033 |
1.29241 |
1.66180 |
|
|
1 |
28.10699 |
83.85794 |
84.71342 |
219.57834 |
140.28768 |
182.13684 |
229.78998 |
278.75371 |
|
|
2 |
0.00287 |
0.00534 |
0.00865 |
0.02728 |
0.00634 |
0.00735 |
0.00833 |
0.00907 |
|
|
2 |
0.14176 |
0.33489 |
0.43243 |
1.27506 |
0.47877 |
0.58858 |
0.70496 |
0.81221 |
|
|
2 |
7.00890 |
21.00679 |
21.60758 |
59.60180 |
36.14519 |
47.13183 |
59.65897 |
72.72299 |
|
|
3 |
0.00353 |
0.00220 |
0.00503 |
0.00891 |
0.00733 |
0.00852 |
0.00961 |
0.01008 |
|
|
3 |
0.08887 |
0.12259 |
0.18738 |
0.44144 |
0.29270 |
0.36066 |
0.43139 |
0.48842 |
|
|
3 |
2.23826 |
6.81691 |
6.98521 |
21.88176 |
11.68365 |
15.27249 |
19.36171 |
23.67305 |
|
|
p |
2 |
0.00764 |
0.01525 |
0.01749 |
0.00941 |
0.00780 |
0.00859 |
0.02872 |
0.02639 |
|
2 |
0.05404 |
0.32359 |
0.44032 |
1.06329 |
0.29523 |
0.34774 |
0.78835 |
0.84922 |
|
|
2 |
0.38239 |
6.86518 |
11.08270 |
120.17749 |
11.17023 |
14.08015 |
21.63916 |
27.33244 |
|
|
3 |
0.00921 |
0.00843 |
0.00836 |
0.01140 |
0.00549 |
0.00604 |
0.00560 |
0.00766 |
|
|
3 |
0.06526 |
0.14110 |
0.18189 |
0.42871 |
0.13807 |
0.16239 |
0.21428 |
0.26619 |
|
|
3 |
0.46268 |
2.36271 |
3.95736 |
16.12051 |
3.47500 |
4.36262 |
8.19443 |
9.24446 |
|
|
4 |
0.00352 |
0.00371 |
0.00390 |
0.00518 |
0.00611 |
0.00673 |
0.00656 |
0.00956 |
|
|
4 |
0.04357 |
0.06433 |
0.08315 |
0.16886 |
0.09101 |
0.10611 |
0.15800 |
0.19305 |
|
|
4 |
0.53982 |
1.11514 |
1.77409 |
5.50665 |
1.35551 |
1.67188 |
3.80271 |
3.89907 |
|
|
d |
3 |
0.00872 |
0.00897 |
0.00909 |
0.00903 |
0.00894 |
0.00888 |
0.00883 |
0.00880 |
|
3 |
0.02464 |
0.02586 |
0.02646 |
0.02614 |
0.02573 |
0.02540 |
0.02517 |
0.02501 |
|
|
3 |
0.06964 |
0.07454 |
0.07701 |
0.07569 |
0.07400 |
0.07267 |
0.07174 |
0.07109 |
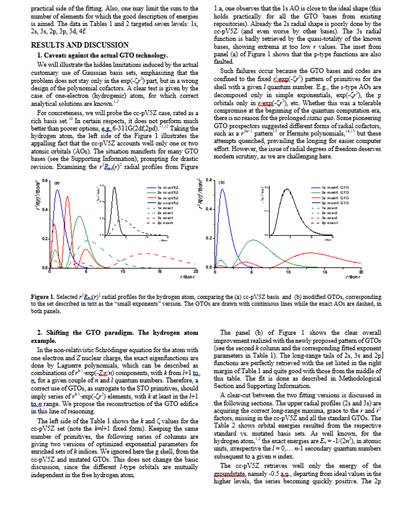
Figure 1. The r*R(r) profiles for the Ne atom, with GTOs. Dashed lines: the results from the 6-31+G* standard basis. Continuous lines: new basis (see Table 1).
We chose to optimize the exponents of the Li-Ne series in in restricted spinless scheme. For the s-type orbitals we convened to use three primitives with k=1, three ones with k=2 and three with k=3, targeting the fit of the 1s-4s orbitals (i.e. two virtuals). For the p shell we considered three primitives for k=2, three for k=3, and also three elements for k=4, fitting the 2p-4p shells. The 3d shell was treated by three GTOs with k=3. The results are presented in the Table 1. The Figure 1 compares the new basis with a consecrated one, 6-31+G*, taking the Ne atom. One observes that, while the occupied atomic orbitals (1s,2s,2p), are similar in both treatments, the new basis enables radially more expanded virtuals, as proven correct in the previous stage of the project.
Adjusting basis sets for the d and f elements by optimization to experimental atomic spectra and Slater-Condon parameters.
Here we continue with Slater-Type Orbitals (STOs), the problem being also approachable with GTOs.
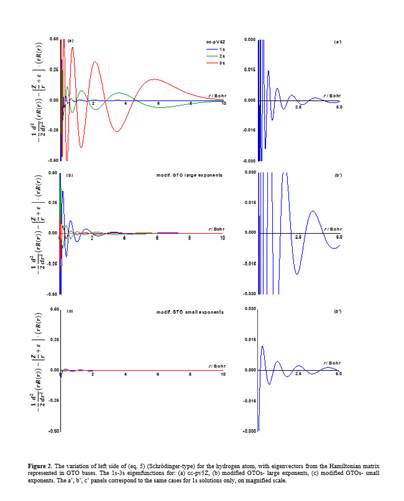
We will take as example for the treatment of the d-type transition elements the case of the Ni(II) free ion. The experimental data of Ni(II) ion (NIST) show a rather visible spin-orbit split of the ground term, 3FJ, with relative values 0, 1360.7 cm-1and 2269.6 cm-1 for respective J=4, 3 and 2 sub-multiplets. The barycentre of this set estimated as the average with the 2J+1 weights, is 993.9 cm-1. Extracting this amount from the energies of other terms (these averaged too, when spin-orbit multiplets appear), the levels are E(1D)= 13037.6 cm-1, E(3P)= 15836.3 cm-1, E(1G)= 22114.7 cm-1 and E(1S)= 51538.0 cm-1. For d elements is convenient to convert the Slater-Condon integrals in the so-called Racah parameters:
,
and 
(2)
The analytic expressions of spectral terms, as function of Racah parameters, from table encapsulated in the Figure 2 can be fitted, by least square procedures, obtaining the B=1154.5 cm-1 and C=3946.6 cm-1 values, rendering the following numeric approximations: Efit(1D)= 13665.8 cm-1, Efit(3P)= 17317.5 cm-1, Efit(1G)= 21747.3 cm-1 and Efit(1S)= 53025.5 cm-1.
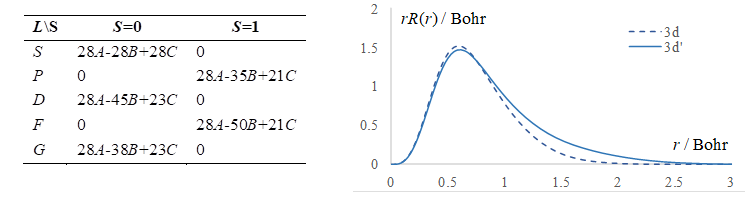
Figure 2. Synopsis of the Ni(II) treatment, illustrative for the d-type elements. Left side: table of analytic formulas for the spectral terms, as function of Racah parameters. Right side: the r*R(r) radial profile of the canonical 3d orbital (dashed line) compared with those adjusted to the retrieval of experimental Racah parameters.
The calculation done with optimized STO yields the B=1214.82 cm-1 and C=4450.47 cm-1 values. This can be adjusted by a remix between 3d and 4d functions, with the {0.99275, 0.12017} coupling, retrieving the B=1092.58 cm-1 and C=3962.27 cm-1 values, close to the experimental set. From the right side of the Figure 2, one observes that the adjusted parameters are obtained with a profile slightly more extended at larger radii (labelled 3d'), as compared with the canonical 3d function.
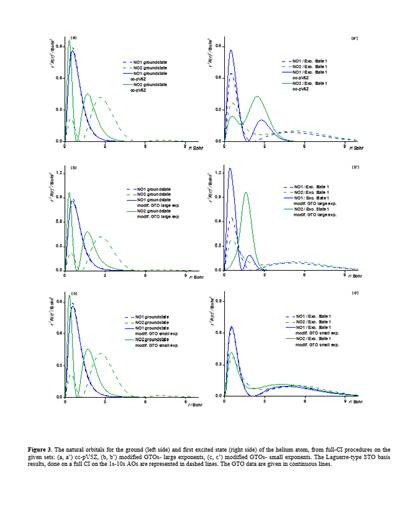
The lanthanide series
will be exemplified by the case of the Nd(III) free ion, performing procedures
similar to those exposed at the above d-metal ion discussion. First, will
consider the experiment data, obtained from the handling of optical multiplets.
All the spin quartet terms and a part of the doublets have simple linear
formulas as function of the Slater-Condon parameters (See left side of the
Figure 3). There are several data available: 4F, 4G and 2K,
relative to the 4I groundstate, at the 10207 cm-1, 16040
cm-1 and 17210 cm-1 barycentres, respectively. These are
sufficient for an estimate the experimental parameters: 
362.79
cm-1, 
44.81
cm-1 and 
6.86
cm-1.
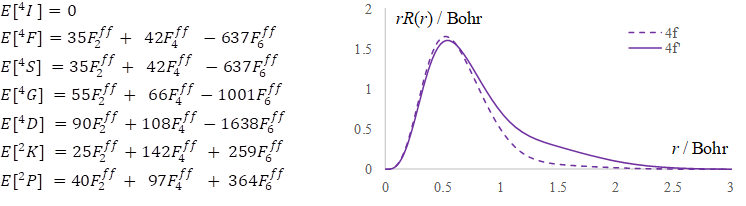
Figure
3.
Synopsis of the Nd(III) treatment, illustrative for the f-type elements. Left
side: Analytic formulas for the spectral terms, as function of Slater-Condon
parameters. Right side: the r*R(r)
radial profile of the canonical 4f orbital (dashed line) compared with those
adjusted to the retrieval of experimental 
parameters.
We
optimized a basis having three STO primitives with k=4 preexponential
factors and the z={0.138, 1.067, 8.277} set of exponents,
aside two primitives with k=5 and z ={0.006, 4.415}. The
canonical 4f orbitals lead to a certain over-estimation of the Slater-Condon
parameters, as in all the above previously mentioned instances: 466.85
cm-1, 60.40
cm-1 and 6.42
cm-1. Proceeding, as previously, to the coupled rotation of the 4f
and 5f orbitals, one achieves a new 4f' shell with 
values closer the
experimental data, 362.81 cm-1, 46.36 cm-1 and 4.91 cm-1,
for the outlined parameters. The right side of the Figure 3 shows that these
results imply a certain "breathing" of the shell, reaching slightly expanded
radial shape. The canonical orbitals have somewhat compressed radial profiles,
as consequence of a compensation effect: the shrunk shape enforces larger
positive energy of inter-electron repeal, while increases the modulus of
negative energy of electron-nuclear attraction. The fit to experimental
parameters of the electronic spectra prepares contracted bases with a better
account of the correlation effects.[4]
Plane Wave methods as source for radial profiles of atomic orbitals. The atomic calculations of lanthanides show several aspects under debate.[5],[6] Specifically, will consider atoms with the 6s25d14fn electronic configuration. Within the considered projected-augmented wave (PAW) computational method, with VASP code,[7] the configuration of lanthanide atoms is [Xe]5s25p26s25d14fn, namely with the electrons of [Xe] core replaced by the effective potentials. In the following we decompose the problem in Slater-type Orbitals (STOs) but the issue is also tractable in GTO terms.
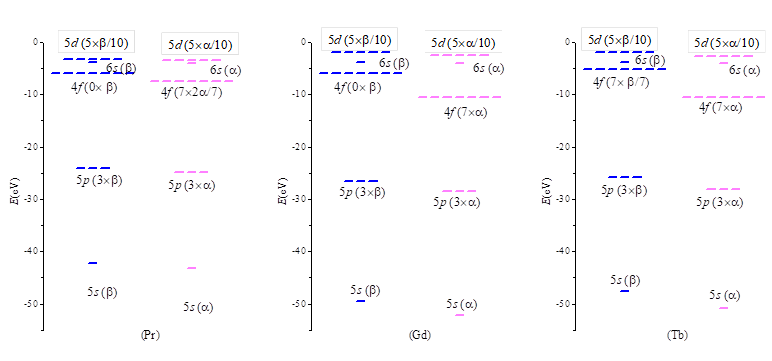
Figure 4. Orbital levels of selected lanthanide atoms, Pr, Gd and Tb, computed by DFT (PBE functional) within Gamma-zero option, with VASP code, under specific control of non-aufbau configuration.
We will consider the spin polarization only for the f shell, while the electrons in 4s and 5d are paired in their shells. In order to keep the spherical nature of the atom, fractional occupations are considered for the incomplete degenerate orbital sets. Namely, for the fn shell, each atomic orbital (AO) should have a n/7 occupation. For the elements in the first half of the lanthanide series (n<7) there are n/7 electrons and empty subsystem. For instance, the Pr(III) ion has the f2 configuration, corresponding to 2/7~ 0.285714 population of each f -type AO. At the middle of the series, the Gd(III) has an integer occupation of AOs, with n=7 and the half-filled f7 shell. After the middle of the series, the f7 configuration is kept, the fractional occupation going into the part. For instance, the Tb(III) ion, with the f8=f7f1 configuration has 1/7~0.142857 electrons in each -type f orbital. In all cases, the outer 5d shell is considered using fractional occupations, spinless, with 0.5+0.5 configuration, e.g. the d1 electron being smeared as 0.5 and 0.5 fractional occupations of each component of the unrestricted d-type shell.
In the figure 4 we selected several cases, such as the Pr, Gd and Tb atoms. Practically, all the systems are non-aufbau, since the upper 5s and 4d orbitals are occupied, above the partly filled or empty f shell components. For the Pr atom, this occurs in both and subsystems (considering the partly filled f2 and the empty f0). At half-occupation (i.e. Gd), or after it (Tb-Yb), the non-aufbau configuration occurs for the f electrons. We managed the non-aufbau calculations with the help of occupation keywords (FERWE and FERDO in VASP). We checked that the non-aufbau sequences, e.g. {1,3,0,1,0.5} for the -{5s,5p,4f,6s,5d} on Pr(III) or Gd(III) are lower in energy than the aufbau series reordering {5s,5p, 6s,5d 4f}, avoiding pushing the empty f shell above the occupied AOs. Since in the lanthanide systems the basic optical and magnetic properties, also interesting for application purposes, are due to atomic-like features it is worth focusing on the detailed study of the f atomic orbitals.
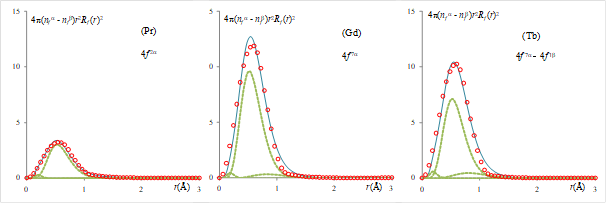
Figure 5. Radial profile of the spin difference density, accounting for 2 electrons in the Pr example, 7 electrons for Gd and 6 electrons for the Tb case (proportional to the area under curves). The results from VASP atomic calculation are shown by circles and the continuous line corresponding to the fit with a combination of three Slater-Type Orbitals (STOs), represented by dashed lines.
An interesting result, extracted from the above calculation, is the radial profile of the spherical section in the volume occupied by the f electrons (see Figure 5). It is obtained from the maps of minus electron densities, representative completely for the f shell. The radial profile from plane-wave calculations allows us to fit the 4f node-less AO as combination of Slater-type orbitals (STOs) and, from here, to estimate the Slater-Condon two-electron parameters, which will provide the Coulomb (U) and exchange (J) parameters to be employed in a DFT+U scheme. Thus, with the following functions:
(3)
the atomic orbitals are obtained as linear combinations of STOs:
(4)
Taking for the 4f shell three components with n=4, for the selected atoms, the resulted parameters are presented in Table 2.
Table 2. Parameters of the f atomic shell subsequently obtained to the plane-wave calculation of selected lanthanide atoms. The coefficients (ai) and exponents (zi) of the three STO primitives fitting the radial pattern and the resulted Slater-Condon electron-electron parameters (Fk).
|
|
Pr |
Gd |
Tb |
|
|||
|
a1 |
0.16784 |
0.10800 |
0.13298 |
|
|||
|
a2 |
0.84917 |
0.80185 |
0.74674 |
|
|||
|
a3 |
0.20868 |
0.19800 |
0.24380 |
|
|||
|
|
|
|
|
|
|
|
|
|
z1 |
11.396 |
11.514 |
11.464 |
|
|||
|
z2 |
4.043 |
4.080 |
4.065 |
|
|||
|
z3 |
1.465 |
2.546 |
2.642 |
|
|||
|
|
|
|
|
|
|||
|
F0(cm-1) |
170997.17 |
171793.78 |
170254.73 |
|
|||
|
F2(cm-1) |
368.15 |
393.86 |
383.14 |
|
|||
|
F4(cm-1) |
48.35 |
52.79 |
51.04 |
|
|||
|
F6(cm-1) |
5.18 |
5.70 |
5.50 |
|
|||
The 4f shell treated by a r3exp(-zr) single exponential leads to the following analytic Slater-Condon parameters:
,
,
,
(5)
The relative ratio of the parameters, in the order of increasing subscript is 26580.8: 66.2:9.1:1. For multi-exponential AOs, the expressions are becoming more complex, but yet tractable. Then, with the fitted radial parameters, the Slater-Condon quantities can be obtained. The calculated values are reasonably close to the experimental ones, particularly considering that the traditional Gaussian-based methods are leading to systematic overestimations of the Fk parameters. The spectral experiments do not enable the F0 parameter (which determines a common shift of all the spectral terms). For the F2, F4, F6 series on Pr(III) the experiment yield the 316.7, 58.7, 5.5 respective values, all in cm-1.[8] This compares well with the estimated 368.15, 48.35, 5.18 amounts (in cm-1). As mentioned, the gaussian based multiconfiguration methods are overestimating the leading F2 parameter, having for instance, for Pr(III), the 439.9, 56.5, 6.0 (cm-1) values with the effective core-type SBKJC basis and 431.8, 55.7, 5.9 (cm-1) with the all-electrons SARC basis.